HEAT INDEX FORMULA (Updated 15 February 2019) The Heat Index "Equation" (or, More Than You Ever Wanted to Know About Heat Index) Lans P. Rothfusz Scientific Services Division NWS Southern Region Headquarters, Fort Worth, TX

When summer spreads its oppressive ridge over most of the United State's Southern Region, NWS phones ring off their hooks with questions about the Heat Index. Many questions regard the actual equation used in calculating the Heat Index. Some callers are satisfied with the response that it is extremely complicated. Some are satisfied with the nomogram (see chart).

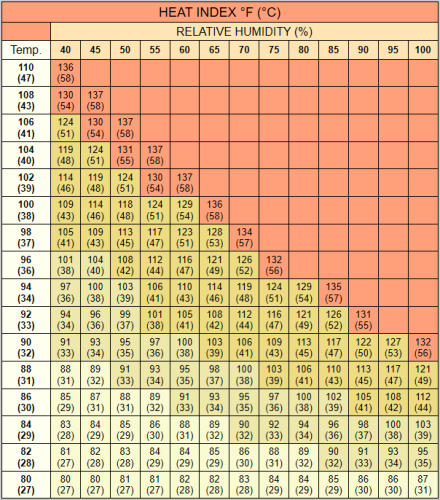
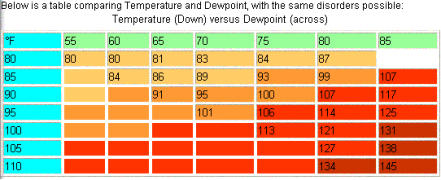
Chart by Lans Rothfusz, MIC at NWS Tulsa, OK

But, there are a few who will settle for nothing less than the equation itself. No true equation for the Heat Index exists. Heat Index values are derived from a collection of equations that comprise a model. This Technical Attachment presents an equation that approximates the Heat Index and, thus, should satisfy the latter group of callers. The Heat Index (or apparent temperature) is the result of extensive biometeorological studies. The parameters involved in its calculation are shown below (from Steadman, 1979). Each of these parameters can be described by an equation but they are given assumed magnitudes (in parentheses) in order to simplify the model. # Vapor pressure. Ambient vapor pressure of the atmosphere. (1.6 kPa) # Dimensions of a human. Determines the skin's surface area. (5' 7" tall, 147 pounds) # Effective radiation area of skin. A ratio that depends upon skin surface area. (0.80) # Significant diameter of a human. Based on the body's volume and density. (15.3 cm) # Clothing cover. Long trousers and short-sleeved shirt is assumed. (84% coverage) # Core temperature. Internal body temperature. (98.6°F) # Core vapor pressure. Depends upon body's core temperature and salinity. (5.65 kPa) # Surface temperatures and vapor pressures of skin and clothing. Affects heat transfer from the skin's surface either by radiation or convection. These values are determined by an iterative process. # Activity. Determines metabolic output. (180 W m-2 of skin area for the model person walking outdoors at a speed of 3.1 mph) # Effective wind speed. Vector sum of the body's movement and an average wind speed. Angle between vectors influences convection from skin surface (below). (5 kts) # Clothing resistance to heat transfer. The magnitude of this value is based on the assumption that the clothing is 20% fiber and 80% air. # Clothing resistance to moisture transfer. Since clothing is mostly air, pure vapor diffusion is used here. # Radiation from the surface of the skin. Actually, a radiative heat-transfer coefficient determined from previous studies. # Convection from the surface of the skin. A convection coefficient also determined from previous studies. Influenced by kinematic viscosity of air and angle of wind. # Sweating rate. Assumes that sweat is uniform and not dripping from the body. As an aside, these assumptions are important for the forecaster to keep in mind. For example, a common perception is that wind is not taken into account in the Heat Index. In actuality it is. It is assumed to be 5 knots. This may seem trivial but a forecaster may be able to use this information creatively when writing Public Information Statements regarding heat stress, heat stroke, etc. # Ventilation rate. The amount of heat lost via exhaling. (2-12%, depending upon humidity) # Skin resistance to heat transfer. A function of activity, skin temperature, among others. # Skin resistance to moisture transfer. A function of the vapor-pressure difference across the skin (and, therefore, relative humidity). It decreases with increasing activity. # Surface resistance to heat transfer. As radiation and convection from the skin increases, this value decreases. # Surface resistance to moisture transfer. Similar to heat transfer resistance but also depends upon conditions in the boundary layer just above skin's surface. These last five variables are used explicitly to derive the apparent temperature. By an iterative procedure which relies on the assumptions in the first list, the model is reduced to a relationship between dry bulb temperature (at different humidities) and the skin's resistance to heat and moisture transfer. Since these resistances are directly related to skin temperature, we now have a relationship between ambient temperature and relative humidity versus skin (or apparent) temperature. As a result of this procedure, there is a base relative humidity at which an apparent temperature (e.g., 90°F) "feels" like the same air temperature (90°F). Increasing (decreasing) humidity and temperature result in increasing (decreasing) apparent temperature, and, yes, apparent temperature can be lower than air temperature. Steadman (1979) developed a table based on this relationship and the nomogram (above) summarizes that table. In order to arrive at an equation which uses more conventional independent variables, a multiple regression analysis was performed on the data from Steadman's table. The resulting equation could be considered a Heat Index equation, although it is obtained in a "round- about" way. Thus, here is an ersatz version of the Heat Index equation: HI = -42.379 + 2.04901523T + 10.14333127R - 0.22475541TR - 6.83783x10 -3T2 -5.481717x10 -2R2 + 1.22874x10 -3T2R + 8.5282x10 -4TR2 - 1.99x10 -6T2R2 where T = ambient dry bulb temperature (°F), R = relative humidity (integer percentage) Because this equation is obtained by multiple regression analysis, the heat index value (HI) has an error of ±1.3°F. Even though temperature and relative humidity are the only two variables in the equation, all the variables on the lists above are implied. References Steadman, R.G., 1979: The assessment of sultriness. Part I: A temperature-humidity index based on human physiology and clothing science. J. Appl. Meteor., 18, 861-873.

HEAT INDEX CALCULATOR